Core 3

Functions

A function is a one to one mapping

Domain and range of a function

The domain of a function is the set of valid input values

A function is defined by both a rule and a domain

Inverse of a function

An inverse function is such that $ff^{-1} (x) = f^{-1} f(x) = x$

For a function to have a valid inverse function, it must be a one to one mapping

Transformations and the modulus function

Translations

Translating the function $y = f(x)$ by the vector $\begin{bmatrix} a \\ b \end{bmatrix}$ gives $y = f(x-a) +b$

$y = kf(x)$ is a stretch of $y = f(x)$ by a factor of $k$ in the $y$ direction

$y = f\left(\frac x k \right)$ is a stretch y a factor of $k$ in the $y$ direction

Reflecting $y=f(x)$ in the y axis gives $y=f(-x)$

The modulus of a function is given by:

| f (x) | = {\begin{cases} f (x) & f (x) \geq 0 \\ - f (x) & f (x) < 0 \end{cases}

$|f(x)| = \left\{ \begin{array}{ll} f(x) & \quad f(x) \geq 0 \\ -f(x) & \quad f(x) < 0 \end{array} \right.$

Inverse trigonometric functions

$\operatorname{asin}(x)$ has domain $-1 \leq x \leq 1$ and range of $-\frac{\pi}{2} \leq \operatorname{asin}(x) \leq \frac{\pi}{2}$

$\operatorname{acos}(x)$ has domain $-1 \leq x \leq 1$ and range of $0\leq \operatorname{acos}(x) \leq \frac{\pi}{2}$

$\operatorname{atan}(x)$ has domain $x \in \mathbb{R}$ and range of $-\frac{\pi}{2} \leq \operatorname{atan}(x) \leq \frac{\pi}{2}$

Trig identities

\begin{aligned} \sin (x)^{2} + \cos (x)^{2} = 1 \\ 1 + \cot (x)^{2} = cosec (x)^{2} \\ 1 + \tan (x)^{2} = \sec (x)^{2} \end{aligned}

$\begin{align} &\sin(x)^2 + \cos(x)^2 = 1 \\ &1 + \cot(x)^2 = \operatorname{cosec}(x)^2 \\ &1 + \tan(x)^2 = \sec(x)^2\end{align}$

Calculus

Log rules

\begin{aligned} \ln (a) + \ln (b) = \ln (a b) \\ \ln (a) - \ln (b) = \ln (\frac{a}{b}) \\ n \ln (a) = \ln (a^{n}) \\ \log_{a} b = \frac{\log_{c} (a)}{\log_{c} (b)} \end{aligned}

$\begin{align} &\ln(a) + \ln(b) = \ln(ab) \\ &\ln(a) - \ln(b) = \ln\left(\frac{a}{b}\right) \\ &n\ln(a) = \ln(a^n)\\ &\log_a b = \frac{\log_c(a)}{\log_c(b)} \end{align}$

Differentials and integrals

\begin{aligned} \frac{d}{d x} e^{x} = e^{x} & \int e^{x} d x = e^{x} + C \\ \frac{d}{d x} e^{a x + b} = a e^{a x + b} & \int e^{a x + b} d x = \frac{1}{a} e^{a x + b} + C \\ \frac{d}{d x} e^{f (x)} = f^{'} (x) e^{f (x)} & \int e^{f (x)} d x = \frac{1}{f^{'} (x)} e^{f (x)} + C \\ \frac{d}{d x} \ln (x) = \frac{1}{x} & \int \frac{1}{x} d x = \ln (x) + C \\ \frac{d}{d x} \sin (x) = c o s (x) & \int \sin (x) = d x = - \cos (x) + C \\ \frac{d}{d x} c o s (x) = - \sin (x) & \int \cos (x) d x = \sin (x) + C \end{aligned}

$\begin{alignat*}{3} &\frac{d}{dx} e^x = e^x \quad &&\int e^x dx = e^x + C \\ &\frac{d}{dx} e^{ax + b} = ae^{ax+b} \quad &&\int e^{ax+b} dx = \frac{1}{a} e^{ax+b} + C\\ &\frac{d}{dx} e^{f(x)} = f'(x)e^{f(x)} \quad &&\int e^{f(x)} dx = \frac{1}{f'(x)} e^{f(x)} + C \\ &\frac{d}{dx} \ln(x) = \frac{1}{x} \quad &&\int \frac{1}{x} dx = \ln(x) + C \\ &\frac{d}{dx} \sin(x) = cos(x) \quad &&\int \sin(x) = dx = -\cos(x) + C \\ &\frac{d}{dx} cos(x) = -\sin(x) \quad &&\int \cos(x) dx = \sin(x) + C\end{alignat*}$

The chain rule

\frac{d y}{d x} = \frac{d y}{d u} \frac{d u}{d x}

$\frac{dy}{dx}\ = \frac{dy}{du} \frac{du}{dx}$

The product rule

\frac{d}{d x} f (x) g (x) = f (x) g^{'} (x) + f^{'} (x) g (x)

$\frac{d}{dx} f(x) g(x) = f(x)g'(x) + f'(x)g(x)$

\frac{d}{d x} u v = u v^{'} + v u^{'}

$\frac{d}{dx} uv = uv' + vu'$

The quotient rule

\frac{d}{d x} \frac{f (x)}{g (x)} = \frac{g (x) f^{'} (x) - f (x) g^{'} (x)}{g (x)^{2}}

$\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{g(x)f'(x) - f(x)g'(x)}{g(x)^2}$

\frac{d}{d x} \frac{u}{v} = \frac{v u^{'} - u v^{'}}{v^{2}}

$\frac{d}{dx} \frac{u}{v} = \frac{vu' - uv'}{v^2}$

Integration by inspection and substitution

\begin{aligned} \int \cos (a x + b) d x = \frac{1}{a} \sin (a x + b) + C \\ \int \sin (a x + b) d x = - \frac{1}{a} \cos (a x + b) + C \\ \int \sec (a x + b)^{2} d x = \frac{1}{a} \tan (a x + b) + C \\ \int \frac{f^{'} (x)}{f (x)} d x = l n | f (x) | + C \end{aligned}

$\begin{align} &\int \cos(ax + b) dx = \frac{1}{a} \sin(ax + b) + C \\ &\int \sin(ax + b) dx = -\frac{1}{a} \cos(ax + b) + C \\ &\int \sec(ax + b)^2 dx = \frac{1}{a}\tan(ax + b) + C \\ &\int \frac{f'(x)}{f(x)} dx = ln|f(x)| + C \end{align}$

Integration by parts and standard integrals

\int f (x) \frac{d}{d x} g (x) d x = f (x) g (x) - \int g (x) \frac{d}{d x} f (x) d x

$\int f(x) \frac{d}{dx} g(x)\ dx = f(x)g(x) - \int g(x) \frac{d}{dx} f(x) \ dx$

More simply

\int u \frac{d v}{d x} d x = u v - \int v \frac{d u}{d x} d x

$\int u \frac{dv}{dx} \ dx = uv - \int v \frac{du}{dx} \ dx$

In general it is easier to make $u$ the simpler part of the given integrand.

Volume of a revolution

The volume of a function $y = f(x)$ rotated fully around the $x$ axis is given by

V = \int_{a}^{b} π y^{2} d x

$V = \int _a ^b \pi y^2 \ dx$

To find the volume of a revolution around the $y$ axis, rearrange the function to the form $x = g(y)$ .

Numerical solutions and iterative methods

Iteration

Iteration requires a formula in the form $X_{n+1} = f(x_n)$

An iterative formula converges if $|f'(x)| < 1$ | for certain values of x

If the iteration converges to a limit the limit can be found by setting $x_{n+1} = x_n = L$

Trapezium rule

\int_{a}^{b} y d x \approx \frac{b - a}{n} [y_{0} + y_{n} + 2 (y_{1} + . . . + y_{n - 1})]

$\int _a ^b y\ dx \approx \frac{b-a}{n} [y_0 + y_n + 2(y_1 + ... + y_{n-1})]$

If $y$ tends upwards the rule will overestimate, and if $y$ tends downwards the rule will underestimate.

Mid-Ordinate rule

\int_{a}^{b} y d x \approx \frac{b - a}{n} (y_{\frac{1}{2}} + y_{\frac{3}{2}} + . . . + y_{n - \frac{3}{2}} + y_{n - \frac{1}{2}})

$\int _a ^b y\ dx \approx \frac{b-a}{n} (y_{\frac{1}{2}} + y_{\frac{3}{2}} + ... + y_{n - \frac{3}{2}} + y_{n - \frac{1}{2}})$

Where $n$ is even.

Simpson’s rule

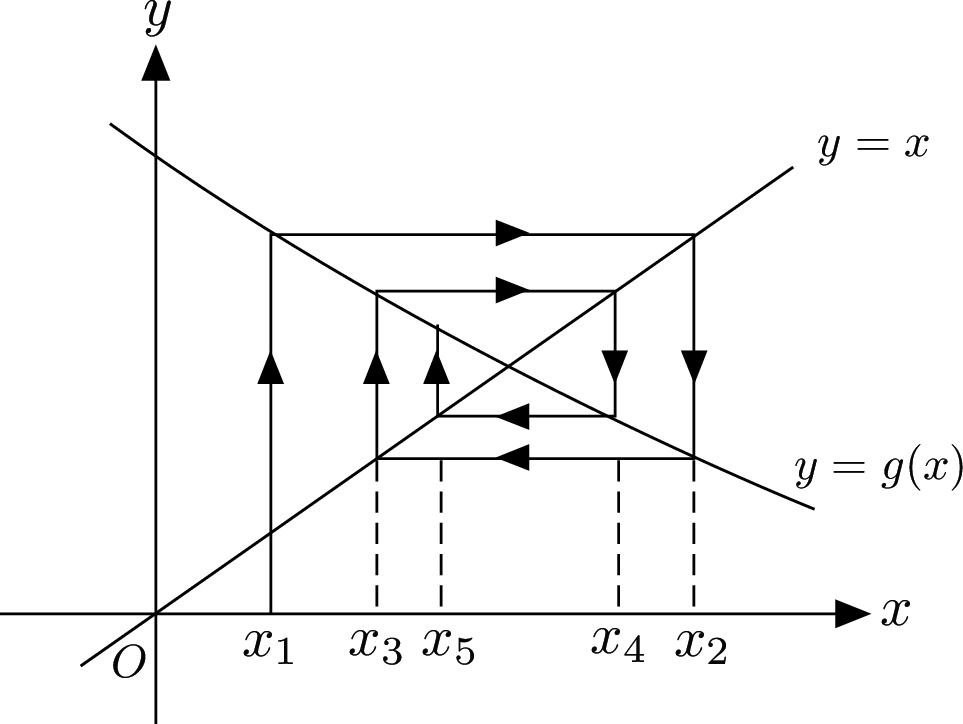
\int_{a}^{b} y d x \approx \frac{b - a}{3 n} [y_{0} + y_{n} + 4 (y_{1} + y_{3} + . . . + y_{n - 1}) + 2 (y_{2} + y_{4} + . . . + y_{n - 2})]

$\int _a ^b y\ dx \approx \frac{b-a}{3n} [y_0 + y_n + 4(y_1 + y_3 + ... + y_{n-1}) + 2(y_2 + y_4 + ... + y_{n-2})]$

Cobweb diagram

Plot the two functions

A cobweb diagram is plotted by drawing up from the first x value, before rotating around, alternating between each of the functions for each value of x.

This is more appropriate when the values converge around the root rather than towards it.

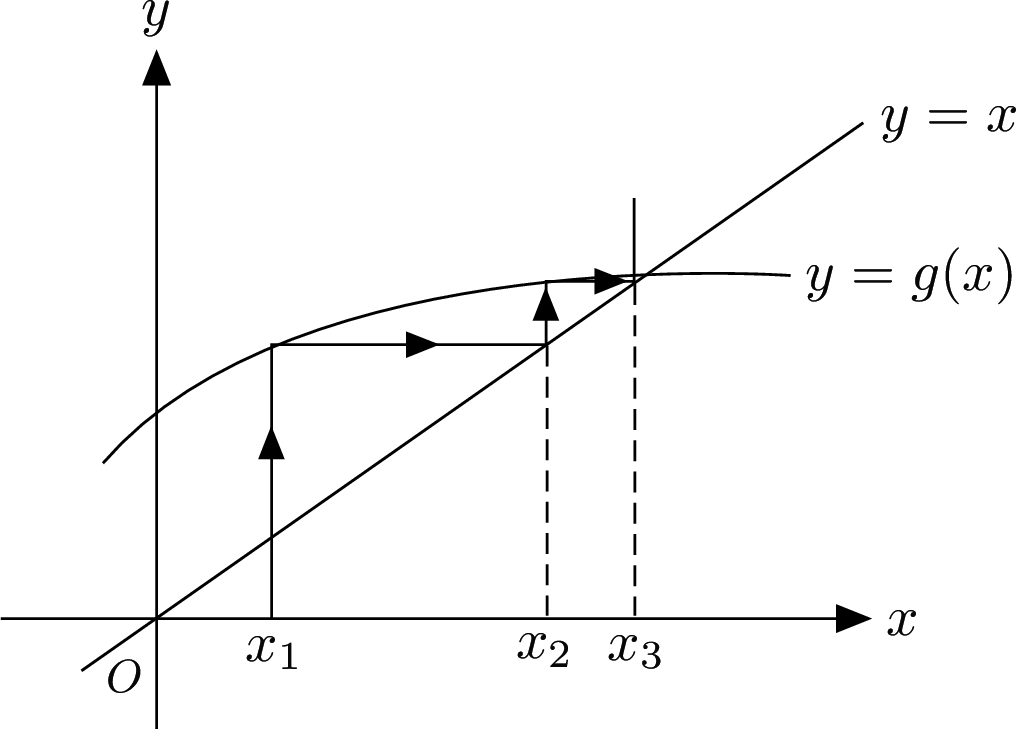
Staircase diagram

Plot the two functions

A staircase is plotted by drawing a line up from each x value to one of the functions, and then drawing across to the next intersect with the other function.